Lamniar vs. Turbulent Air Flow

As a fluid flows around an object, the fluid can do one of two things. The flow can stay more or less in tact as it run into and around the object causing some drag, which we call a laminar flow. Or the flow can build up chaotic flow bits like eddy currents which increase the drag, which we call turbulent flow. In the visualization below, the flow shown in red above the cube is more or less laminar in nature, but the flow behind the cube seems more turbulent.

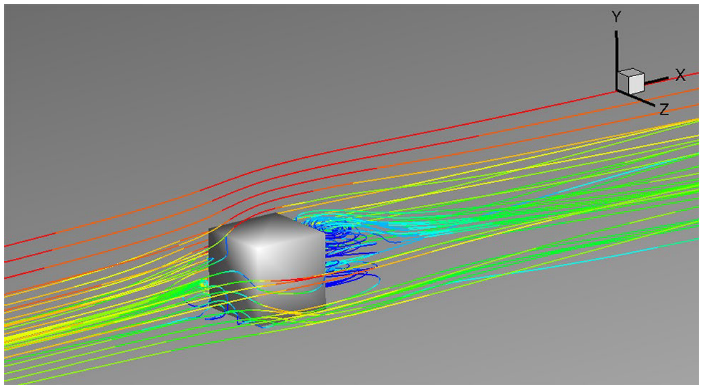
Fluid Flow around a Cube from Schröder et al., 2020

For laminar air flow we can model air drag as a drag coefficient times the speed at that moment:

The drag coefficient, b, is a dimensionless quantity dependant on the fluid properties and the object geometry. We will be using coefficients ranging from 0.2 to 1.0.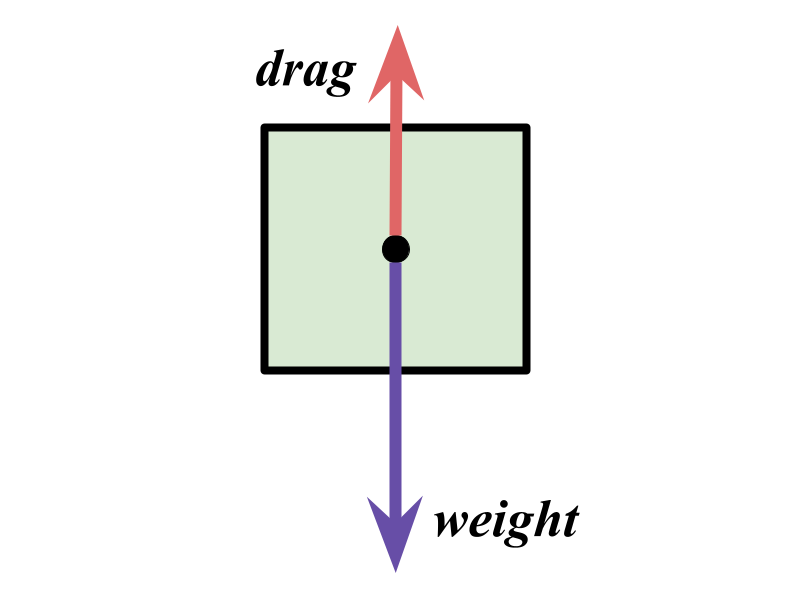

Free Body Digram with Drag Force

The sum of the forces on the center of mass of the block is given by:

We can solve this expression by integration through separation of variables:

After some time passes we will reach the terminal velocity:

This is the final expression for velocity as a function of time for an object experiencing laminar air drag from the time the object was dropped until it hits the ground:

Now It's Your Turn

For comparison, you will create a realistic model of how terminal velocity depends on the drag coefficient of an object.

Step 1: Make the objects fall with ONLY gravity.

Open the code in the editor. Drag Lab Starter Code

Look at this line in sketch.js inside the draw function. What can you put there to make the object experience freefall? Test that out and make sure it seems to work correctly. How do you update the y-velocity of the objects? How do you update the position of the objects?

    // 1.0 is the mass of the object
    a1 = 0;

All 6 objects should be falling due to gravity like this. 

Step 2: Complete the air drag acceleration function.

Notice there is a function called a_drag(...). You will need to complete this function to return the acceleration acting against the acceleration due to gravity. How can you take the drag force formula and turn it into the drag acceleration formula? Hint: think of Newton's 2nd law in its most famous form!

function a_drag(v, b, m){
    a = 0; // fix this line

    // Do not exceed acceleration due to gravity!
    if (a > abs(g)) a = abs(g);

    // Return the acceleration due to drag
    return a;
}

Step 3: Test your code for the first object. Does it seem to experience air drag?

Try adding this line to update the acceleration rather than letting the object fall just due to gravity. Note that this program uses 981 cm/s^2 for g, the acceleration due to gravity. Positions are also modeled as centimeters here.

// 1.0 is the mass of the object
a1 = g - a_drag(vy1, 9.0, 1.0);

Run the code and see if you can tell the difference between the time it takes to fall with and without air drag.

Step 4: Add the other 5 objects to the code.

Be sure to add lines to update acceleration, velocity, and position of the other 5 objects. Be sure to update the mass by 1 for each added box. Use 9.0 for the drag coeeficient, b, for all the objects. Don't forget to call drawBox(...) for each object!

If all is well, you should see code that works like this.

Step 5: Open the Javascript console and copy your data

The sketch you ran has the position and time data from the simulation available. You need to open the Javascript console in your browser and copy all the rows and columns of data. 

Next, open a spreadsheet like Excel or Google Sheets and copy and past the data into the spreadsheet. Clean up any weird things so only the times and positions are left.

Step 6: Determine whether this data is laminar or turbulent

Using the data in your spreadsheet, determine the terminal velocity of each of the objects using the position and time data. Then linearize the terminal velocity versus weight data such that the slope of the linear can show that the drag is either laminar or turbulent. Turn in the spreadsheet with your results and plots.